20241025_ISM
电离气体的压强平衡
伴随较高温度的是较大的压强
所有的粒子具有一个 distribution function $f(\vec{x},\vec{p},t)$,满足 Boltzmann 方程
假设粒子是无碰撞的,则有
用 Lagrange 方法分析,限定一个粒子 group 而不限定区域。
可以将流体分为很多微元进行分析,微元的尺度大于碰撞 mean free path,在这一尺度之上粒子的运动速度近似由温度决定
(cgs 单位制)
- 对于恒星来说,mfp 大约是 10nm.
- 对于 stellar wind, mfp 是 pc 量级,可以视作无碰撞的流体
- particle in cell simulation
- cluster 中的 ICM 温度很高,足以产生可以和引力相平衡的压强(用引力势来计算温度,称为 virial temperature)
- 虽然 mfp 是 0.1 Mpc,但是 ICM 尺度更大(100 Mpc)
流体力学基本方程 #
质量守恒 #
(Euler view)
随动导数定义为
动量守恒 #
第二项是对并矢求散度,第三项中 $P$ 也是一个张量。
能量守恒 #
其中 $\gamma$ 蕴含物态方程的信息。
对于单原子理想气体之外的其他介质,$\gamma$ 的值大约在 $1\sim 5/3$ 之间。
声波传导 #
假设介质初始处于 $\rho_0,\vec{u}_0=0$ 的状态,增加一个微扰并研究一阶近似。
其中 $c_s^2=\frac{\gamma P_0}{\rho_0}$ 是绝热声速,描述密度扰动传播的速度。
Shock Wave #
密度较大的地方声速也比较快,使得波形变得更加 sharp;在 shock wave 两侧物理性质出现突变
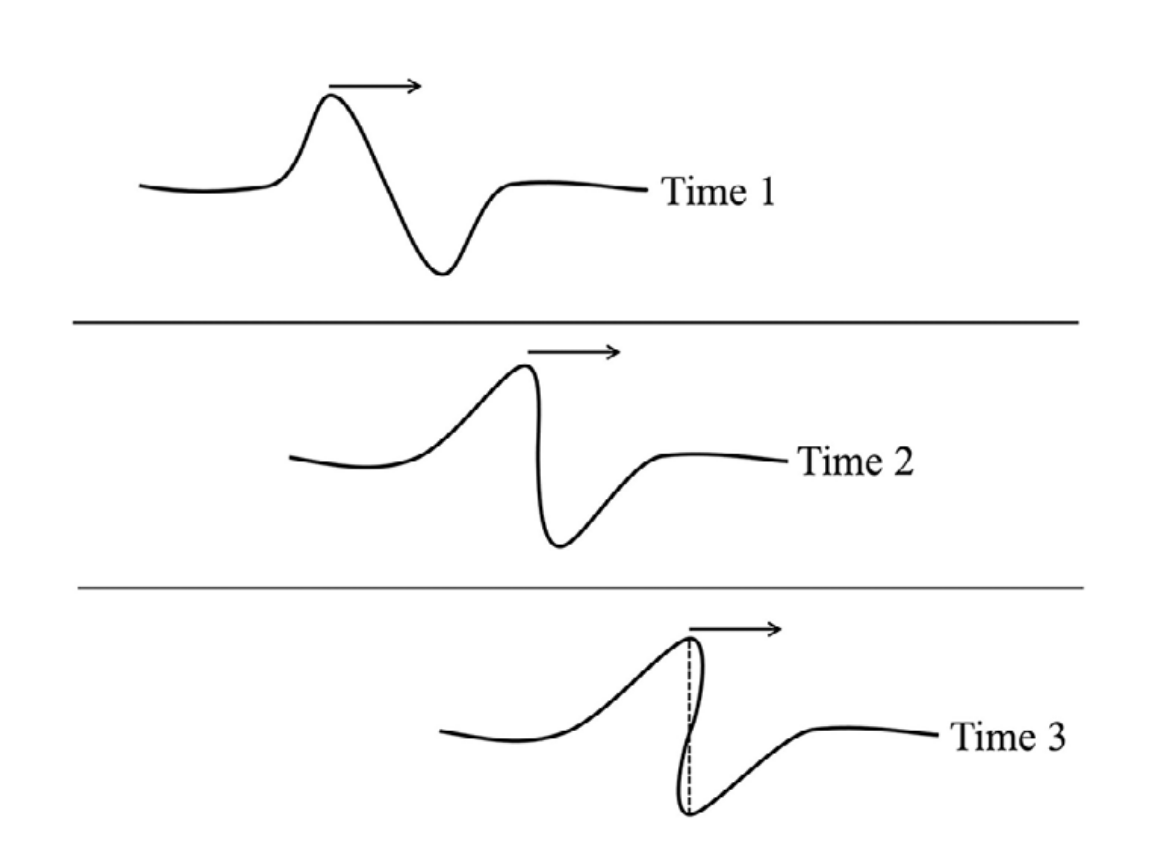
Supernovae #
激波是密度的传播。
激波两侧的物理性质用 $\rho,P,T$ 描述。如果建立随 shock wave 运动的参考系,wave 两侧的物理性质不随时间变化。
其中 $E=\frac{1}{\gamma-1} \frac{P}{\rho}$.
Mach number 用于描述粒子速度和声速的比值
可以算出 $\rho,P,T,u$ 等物理性质在 wave front 前后的比值和 Mach number 的关系。对于 supernovae,Mach 数非常高。这种情况下可以进行近似
波后的速度是波前的 4 倍,但是可以产生很高的波后温度和压强。
对于波后的高温,冷却速度非常快。假设波后的冷却非常有效,激波两侧的能量守恒被打破,也就是 $T_3=T_1$.(这种情况下的激波称为辐射激波)
辐射激波的压缩倍数(密度之比)可以达到 100~1000 量级。对于具有高 mach number 的气体,cooling 效率又降低,所以压缩倍数存在一个上限。
辐射激波可以造成恒星形成的链式反应。
Supernovae Remnant #
考虑 non-radiative spherical shock wave
超新星爆发产生的 shock wave 导致碰撞电离,并且造成电离发射线。
一个简单的物理模型:短时间向很小的区域内注入大量能量
爆发时,除中心铁核之外,外围包层(典型质量为 10 solar mass)以 ejecta 的形式向外扩散(3000~5000 kms)(典型能量为 1e51erg,核聚变炸弹的能量为 1e20erg)
Free-expansion Phase #
shock wave 的速度不变($r\propto t$)
结束的标志是 ejecta 质量和被带动的 ISM 质量近似
对应的典型半径约为 4.1pc,时标为 100yr 量级。
Sedov–Taylor Phase #
超新星爆发的重要属性是能量、周围介质的密度,无法构造出特征的时标和尺度,这是一个 self-similar system;演化和时间是相关的
Sedov-Taylor solution:
典型的膨胀过程是 $t=10^3\text{yr}$,$r=5.3\text{pc}$.
Snowplow Phase #
扫雪机/雪耙
标志是 shell density 非常高,中心压强驱动 wave 的传播
可以近似为绝热膨胀过程,冷却依靠对外做功。
H II 的激波 #
对于高温电离区,也会产生激波,但是和 supernovae shock wave 相比很弱