Xin Qiao

/home

/tools

/obsidian

~/Obsidians/ Rykoff2014RedMaPPerAlgorithmSDSS

Rykoff2014RedMaPPerAlgorithmSDSS

涉及算法细节的章节是 sec3~sec9

“自训练”的意思就是算法包括很多的参数，然后根据最后的结果调整这些参数，就像 R09 里面的 richness-radius 关系的参数：有点类似一个可解释的算法加上一点机器学习的优化？

Comment #

  • 第三节给出了整体的 outline
    • 用星系样本得到 red sequence 作为红移的函数，然后用 red sequence 识别图像中的 cluster
    • 总之最后的结果就是 detect 到一些 cluster，副产品是一个作为红移的函数的 red sequence
  • 很经常地使用迭代方法，但是迭代是否有效、最后能否收敛其实都是很脆弱的问题
    • 本质上来说是一个统计信息处理和提取的过程，难道没有更优雅的方法吗？
  • 这里 section 的顺序到底是按照什么来的？感觉逻辑很混乱
    • sec3~9 应该合并到一起，作为算法原理
    • 应该是 sec6 和 sec9 放在最前面，然后 4,5,7,8 作为这两节的 sub-section
    • 作者的逻辑可能是 4/5 作为 6 的准备工作，7/8 作为 9 的准备工作

Abs #

  • 一个 red sequence cluster finder，优点包括
    • self-training
    • 处理不同深度的 mask
    • 以概率形式给出红移
    • 以概率形式给出 BCG
  • 应用在 10000 平方度的 SDSS DR8 上面，得到了 0.08~0.55 红移上的 25000 个 cluster 的目录
  • 红移的中位误差在 0.02 左右

1 Intro #

主题是 photometric cluster finding

用星系团研究 DE: DES, Pan-STARRS, HSC, LSST

  • 对于多波段数据，可以用算法研究角位置、颜色、红移空间中的 clustering, 算法包括两类
    • 基于光度红移
    • 基于 cluster red sequence
  • new photometric cluster finding algorithm 的必要性
    • 一致性问题
      • 对于 photo-z, faint end 的误差会极大增加，因为没有很好的训练样本
      • 对于 red sequence，4000A break 的位置会随着红移变化，所以需要用不同的颜色来描述 red sequence 中统一的红色
    • 算法应该具有 self training 的能力，因为先验参数的设置可能会导致系统误差
    • numerical efficiency
    • survey mask
    • 这里的 random point 指的是 mock？
    • 为每一个 cluster 生成红移的概率分布，以及 cluster 中心位置的概率分布
    • 最小化 richness-mass 关系的 scatter
      • 在 R09 和 R12 中进行了探索，哪些改进是有效的，而哪些是不重要的
        • 为每一个星系估计 BCG 概率是重要的，而 hard color cut 是不好的
  • 我们提出了 red-sequence Matched-filter Probabilistic Percolation (redMaPPer)
    • 满足以上的要求（具体描述在 2012 年的文章中）
    • 一个 personal bias 是：based on red-sequence，而不使用 photo-z
      • 二者的区别是使用颜色来确定视线方向上的 clustering，而不是直接使用红移空间
        • redMaPPer 也可以用于在红移空间中使用
      • 两种方法的对比
        • 我们不相信 photo-z 在 faint 环境下的效果，因为缺乏训练的样本
        • cluster 中的星系是特殊的，用整个 galaxy population 推测红移是不合理的
        • 过去的比较没有证明 red sequence 方法和 photo-z 哪个是更好的
        • 在足够高的红移下，red sequence 消失，只能使用 phot-z 方法
        • redMaPPer 也需要光谱 sample，但是不需要局部有代表性的样本，可以是各个红移上最亮的星系
    • 只需要 photometric galaxy catalog multi-band 覆盖了对应红移的 4000A break
  • This work 介绍了将 redMaPPer 应用于 SDSS DR8 的结果作为示例
  • 这里提到了 cosmology 的设置：h=1.0 means 全部距离都带有 $h^{-1}\ \mathrm{Mpc}$ 的单位

2 Data #

2011 年的 DR8 数据，覆盖了 14000 平方度

这里使用的星系 catalog 范围和 BOSS 一致（10500 平方度），bad/bright mask 也来自于 BOSS

  • BOSS 提供的 bright star mask 基于 Tycho catalog，是不完全的
    • 和 Yale bright star catalog 对比，有 70/9000 的亮恒星是不在其中的
    • 对 63 个 NGC 天体和以上 70 个亮恒星进行了 mask，除去了 36 平方度的面积
  • redMaPPer 需要非常干净的 galaxy catalog，所以需要严格筛选
    • 这里的策略和 Sheldon12 类似
    • 用 SDSS 默认策略进行 star/galaxy separation
    • 限制 i 波段星等比 21 更亮
    • 剔除具有 SATUR CENTER, BRIGHT, TOO MANY PEAKS, (NOT BLENDED OR NODEBLEND) 的对象
    • 保留了 SATURATED, NOT CHECKED, and PEAK CENTER 的对象
      • 因为 cluster 中心可能会错误地带有这类标签
  • 采用 i-band CMODEL MAG 作为 mag 的描述，但是采用 MODEL MAG 计算颜色
  • 最后进行 extinction correction

需要使用光谱数据来校准 red sequence（但是算法是可以自训练的）并且验证测光红移

使用 SDSS DR9 光谱，20% 用于训练，80% 用于验证

3 Algorithm #

核心参数是：optimized richness estimator $\lambda$

  • 算法分为两个阶段
    • 校准阶段：校准 red sequence 作为红移的参数（其实是得到颜色作为红移的函数 $c(z)$？）
    • finder 阶段：利用校准后的 red sequence（其实就是颜色-红移关系）识别 cluster 以及测量 richness
  • 两个阶段互相迭代
    • 最初的 cluster 来源于 color cut
    • 最初的 red sequence 来源于一批具有光谱红移的 cluster 中心星系
    • 用 cluster catalog 校准 red sequence, 用 red sequence 进行新的 cluster finding
  • 用 cluster 确定 red sequence 的 calibration 过程也是迭代的
    • 在 sec6 中详细介绍
    • 首先用具有光谱红移的 training clusters 进行校准
      • 也就是得到 $c(z)$ 关系
      • 在 maxBCG 中使用的是 SDSS LRG
    • 对于训练集的要求是：每 0.05 红移区间有 40 个具有光谱数据的 cluster
      • 对于 SDSS 能够满足，但是未来的高红移巡天（比如 DES）不一定可以满足
  • 对于 this work
    • 首先从光谱星系中选出一些红色的样本作为 seed, 寻找周围区域的相同颜色星系的 overdensity
      • 通过这种方式将已知的光谱红移扩展到成员星系上，之后可以更精确地确定 red sequence
    • 然后将这些 over-density 视作 cluster 进行 red-sequence 的拟合
      • 这里包含了 tilt，也就是颜色和光度不是独立的
    • 上面两步包含在 sec6 中
    • 基于 red-sequence model 进行 cluster finding (sec9)
      • 将每一个星系假设为 cluster 中心
      • 用 red sequence 计算星系的测光红移 $z_\mathrm{red}$（sec7.1）作为红移的 initial guess
      • 基于红移计算 richness $\lambda$ 以及 likelihood（sec4）
      • 对 cluster member 和红移进行迭代的优化（sec7.2）
      • 根据 likelihood 对 cluster 进行排序，对于排序较高的 cluster 的周围 neighbor 进行 mask，这一过程称为 percolation（sec9.3），可以避免重复计数

4 Richness estimator #

基本和 R09 相同，相比 R12 从 single-color 变成了 multi-color

最基本的想法是对于给定的星系属性，观测到的投影分布是 cluster member 和 background 的相加，richness 应该满足

$$ \lambda = \sum p(\mathbf{x} | \lambda) = \sum_{R < R_c(\lambda)} \frac{\lambda u(\mathbf{x} | \lambda)}{\lambda u(\mathbf{x} | \lambda) + b(\mathbf{x})} $$
  • 其实这个方程的本质就是：为测量到的 galaxy count 乘一个因子得到真正的 cluster member 数量，这个因子由 source 强度和 bkg 强度的比值决定
  • 需要定义半径和光度的 cutoff, 这里 $R_c$ 由 radius-richness 关系给出，光度的截断定义为 $0.2L_\star$
    • radius-richness 关系中有两个参数 $R_0$ 和 $\beta$，采用 R09 中的最佳参数（这里从 $\alpha$ 改成 $\beta$ 是为了和下面 luminosity function 中的参数作区分）
  • 通过数值方法可以直接求解以上方程得到 richness（这一步应该属于 finder 过程），此外还可以得到一个半径的估计 $R_c$
  • 星系的性质 $\mathbf{x}$ 包括到星系团中心的距离、星等、颜色（三个波段）
    • 这里的颜色被压缩到一个 $\chi^2$ 变量中，用于描述 red sequence 的拟合 goodness，或者说是这个星系和模板之间的差距，详情见下面的 color filter 章节
    • 星等分布用 Schechter function 描述，这里参数 $\alpha$ 取值为 1，$m_\star$ 用一个复杂的多项式表示
      • 在未来的 redMaPPer 中，使用 data 的测量值替代这些先验决定的参数

Color filter #

这里关于颜色的 filter function 不再是 Gaussian 形式，而是用 $\chi^2$ 分布来表征

  • 理论 red sequence 模型可以用 $\mathbf{c}(z,m_i)$ 表示，也就是给定红移和星等存在一个唯一的颜色向量
    • 这里考虑了 red sequence 的斜率
    • 用一个协方差矩阵描述离散度
      • 因为颜色包含多个分量
      • 仅和红移有关，和星等无关
  • 对于一个实际的星系来说，$\chi^2$ 的计算方式为 $\chi^2(z) = (\mathbf{c} - \langle \mathbf{c} | z, m_i \rangle) \left(\mathbf{C}{\mathrm{int}}(z) + \mathbf{C}{\mathrm{err}} \right)^{-1} (\mathbf{c} - \langle \mathbf{c} | z, m_i \rangle)$
    • 这里误差包含 intrinsic 的以及测光的误差
  • 如果星系是 cluster 成员，上面的 $\chi^2$ 应该服从 $\chi^2$ 分布
    • 自由度 $\nu$ 为颜色的数量

Background #

假设背景是空间位置无关的，仅取决于星等、颜色和红移（颜色用 $\chi^2$ 描述）

5 Mask/Different Depth #

这一章在逻辑顺序上不是应该在最后吗？

两个限制因素：

  • 在不同的区域上具有不同的 depth
    • 也就是因为深度不足导致没有发现 cluster
  • 存在一些因为 bright star 导致的 mask

估计由于以上因素导致的缺少的 cluster richness 比例，然后进行修正

5.1 Correction term #

将星系参数空间划分为无穷小的 pixel（用 $N_i$ 表示）就可以得到

$$ 1 = \sum_{i} N_i \frac{u(\mathbf{x}_i)}{\lambda u(\mathbf{x}_i) + b(\mathbf{x}_i)} $$

然后拆分为 in 和 out 两部分

$$ 1 = \sum_{\mathrm{in}} N_i \frac{u(\mathbf{x}_i)}{\lambda u(\mathbf{x}_i) + b(\mathbf{x}_i)} + \sum_{\mathrm{out}} N_i \frac{u(\mathbf{x}_i)}{\lambda u(\mathbf{x}_i) + b(\mathbf{x}_i)} $$

前者是实际的观测值，而后者是修正项 $C$

6 Calibration stage #

6.0 Summary #

  • iteration 0
    • 从 SDSS 的光谱星系中选出一些红色的光谱星系
    • 计算颜色-红移关系
  • iteration 1
    • 以星系样本和颜色-红移关系为基础，进行周围成员星系的搜寻并且估计 richness（单色）
    • 用这些星系作为样本得到 red sequence 的第一次估计
  • iteration n
  • 运行 finder 然后再重新计算 red sequence model（在 sec9 中描述）
  • 继续进行迭代，得到 cluster catalog 以及 multi-color membership
    • 在后续迭代的过程中，使用 multi-color 代替第一次迭代中用到的 single color

这里其实包括了整个过程，只不过把基于 red sequence 运行 finder 的过程打包放到 sec9 了

6.1 Outline #

这里对应于第一个阶段也就是 calibration: 从已知红移的 cluster 目录得到 red sequence

这里 cluster 的作用是将中心星系的光谱红移扩展到周围的 member galaxy 上

  • 如果有一个已知光谱红移的星系样本，就可以从中拟合出颜色-红移关系
    • 但是存在限制条件：暗端的星系数据不完全，在校正 red sequence 的斜率上存在困难（很需要这个 tilt 吗？）
  • 一个解决办法是 cluster 将成员星系和中心星系的红移联系起来，只需要一个已知光谱红移的 cluster catalog
    • member galaxy 可能没有光谱数据，但是可以通过 cluster 的性质确定其红移
    • 可以通过 X-ray 或者 SZ catalog 获得，或者用 redMaPPer 先找一些 cluster 出来，然后对其中心进行光谱观测
  • This work 中我们用现有的光谱星系作为 seed，先进行 cluster 的搜寻（通过寻找类似颜色的星系的 over-density），然后进行 red sequence 或者说颜色-红移关系的确定
    • 这些光谱星系一定是 BCG 吗？一定是 cluster member 吗？

6.2 Selecting Seed Galaxies and the Initial Color Model #

calibration 的第一步是从 SDSS 光谱星系中选出作为 seed 的红色星系，这可以通过颜色 cut 来实现（在 0.35 以下用 g-r, 在 0.35 以上用 r-i，以保证跨越 4000A break）

筛选步骤具体来说是

  • 首先把星系按照红移分组（宽度是 0.05）
    • 在程序里面使用的是 0.1
  • 然后估计 red sequence 的颜色平均值和 intrinsic scatter（使用 Gaussian Mixture Method），位于平均值附近 2sigma 以内的星系被认为是红星系
  • 对于这些筛选出来的红色星系，计算颜色-红移关系作为对初始关系的校正
    • 其实有点像 sigma clip
    • 用 spline interpolation 进行拟合
  • 估计 color-redshift 关系的 width，作为对初始 scatter 估计的校正
  • 用更新之后的 mean 和 width 进行再一轮的筛选，筛选标准是 2sigma 以内

这里没有提到颜色和光度的关系

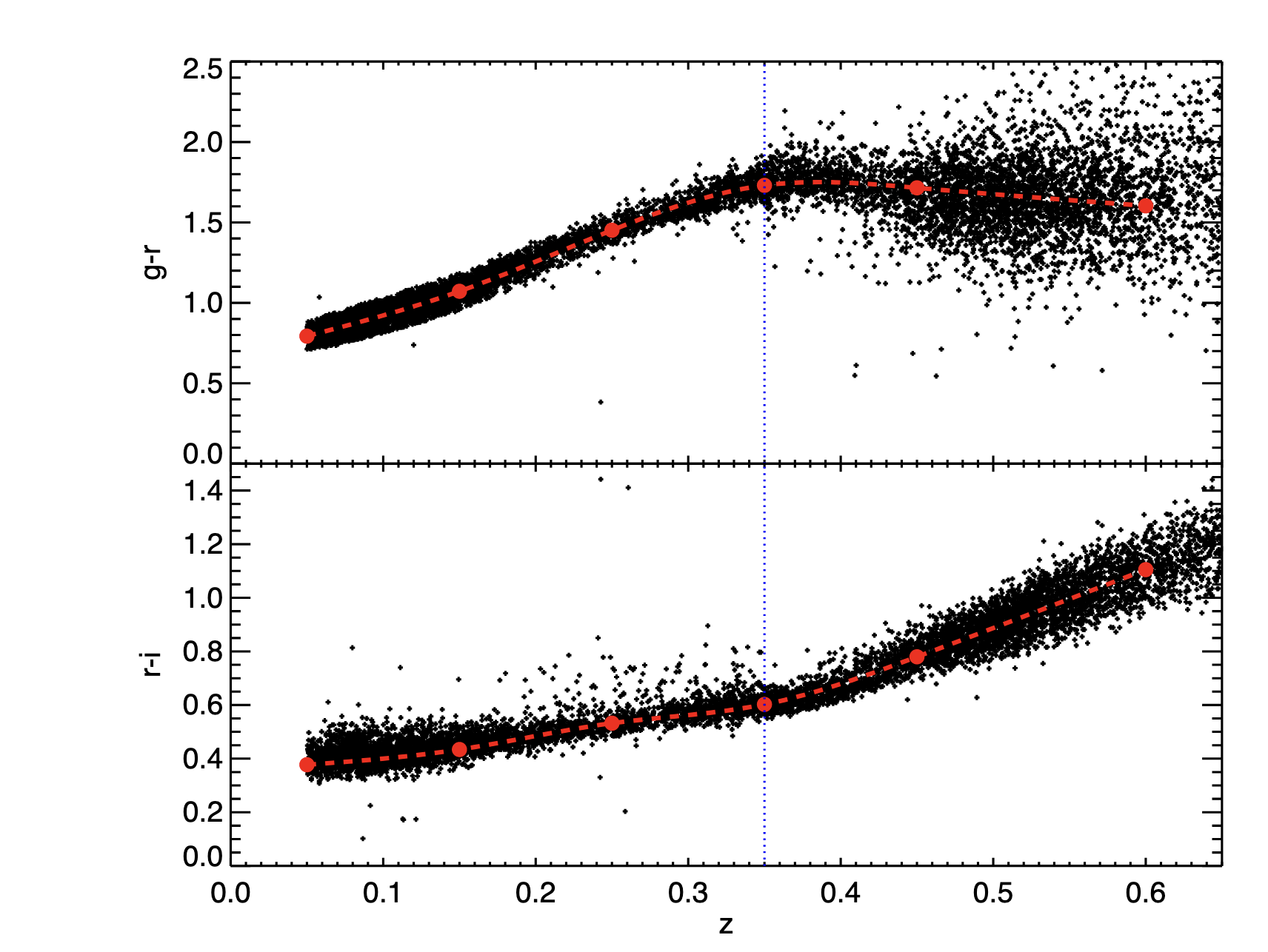
Rykoff2014RedMaPPerAlgorithmSDSS_2.png

这里可以看出红移高于 0.35 之后，g-r 颜色不再变得更红，说明 4000A break 已经越过了 g-r 的窗口？

6.3 Single color member selection #

以上得到了 seed galaxy sample 和初步的 color-z 关系，下面用 single-color 进行周围 member galaxy 的筛选（仅在第一次迭代中使用 single color）

需要注意的是使用 galaxy color 可能在高红移带来噪声，所以这里以颜色-红移模型中的颜色作为 color box 的基准

对于一个 seed：

  • 选取所有位于 seed 周围 $500h^{-1}$ kpc 之内、并且颜色不显著偏离模型颜色 $2\sigma$ 的星系（这里 $\sigma$ 用的是固定值？）
    • 这里的 aperture 是固定的
  • 以这些星系为样本对 red sequence 进行拟合
    • 这里的拟合是为了之后计算 richness 吗？
  • 测量 single-color cluster richness $\lambda$
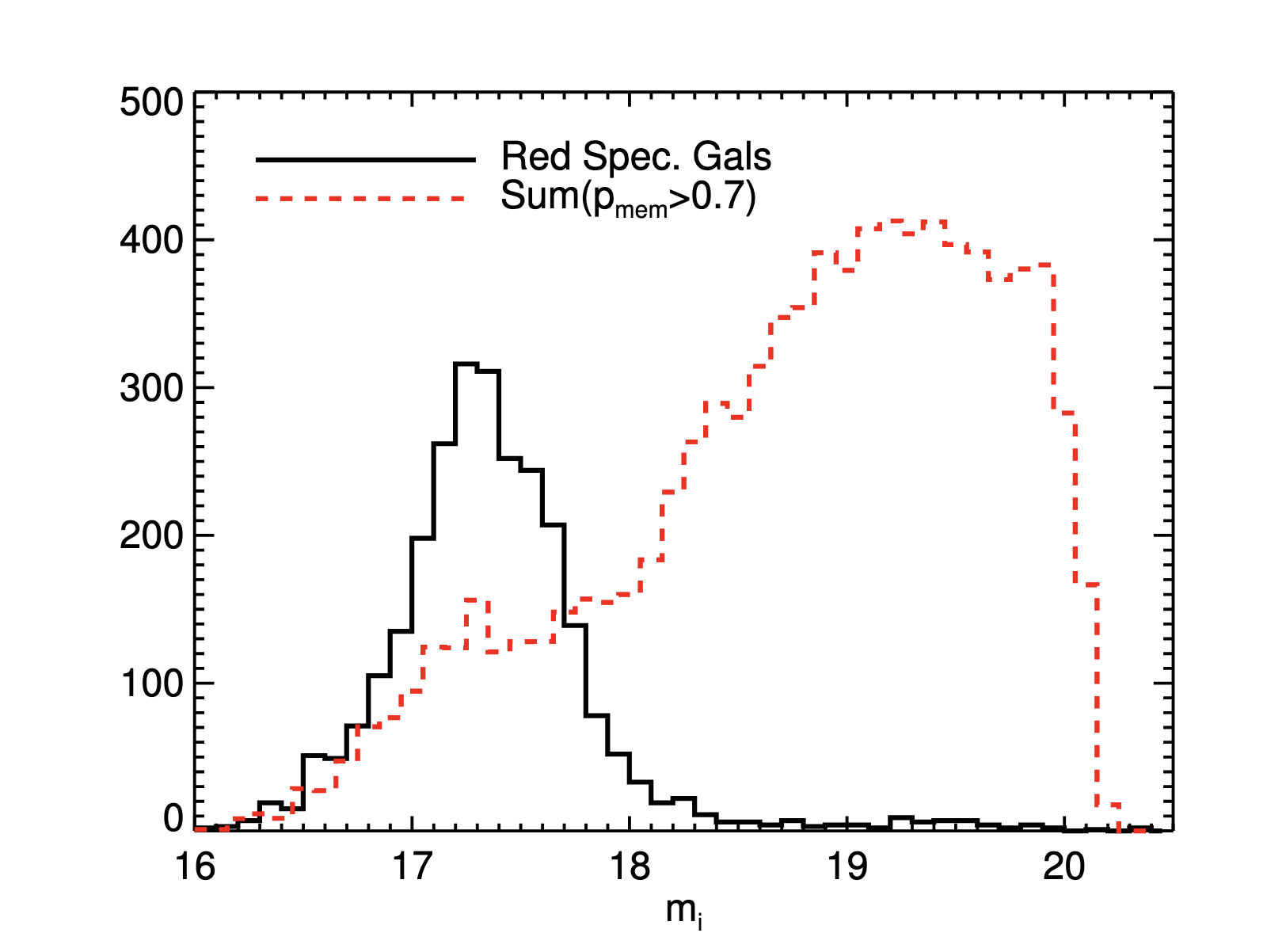
  • 对于 richness 超过 10 的 cluster，将光谱星系的红移赋予周围 membership 大于 0.7 的星系
    • 这样就得到了更大的具有红移的星系样本
    • 虽然这个样本是存在污染的（membership 低于 1），但是其污染程度可以被估计

初始的 seed (42000) 几乎都是较亮的星系，而最后的样本（600,000）中具有更暗的星系。这种向 fainter end 的延伸是依靠对 cluster member 红移的传播实现的。

Rykoff2014RedMaPPerAlgorithmSDSS_3.png

6.4 Modeling the red sequence #

上面用分配红移的方法给一些没有光谱红移的成员星系分配了红移

虽然计算 cluster richness 的时候校准过一遍 red sequence，但是这里用新的星系样本进行再一次校准

  • red sequence 模型由星等-颜色关系来描述
    • 这个关系同时也是红移的函数
    • 除此之外还有 multi-color 对应的协方差矩阵，与单色情况下的 red sequence intrinsic scatter 对应
    • 具有很多的自由参数，警惕过拟合
  • 每次用一种颜色对红移进行校准，之后再拟合协方差矩阵的非对角元素
  • 为了减弱 blue cluster galaxy 的影响，在拟合之前进行一次 color cut
    • 作为弥补需要用截断的 Gaussian 来进行概率计算

6.4.1 Measuring the Model Mean and Color Scatter #

  • 拟合的目标是 $\langle c|m,z\rangle$，也就是给定红移和星等处的平均颜色
  • 首先找到一个中位星等作为 pivot point，然后校准某个红移处 red sequence 的斜率和截距
  • 通过一定的颜色 cut 来避免蓝星系的影响
  • 最后还计算了单一颜色对应的 scatter，用 $C_{jj}^{\mathrm{int}}(z)$ 表示
  • 最后得到了更加精确的红移-颜色关系，如下图所示

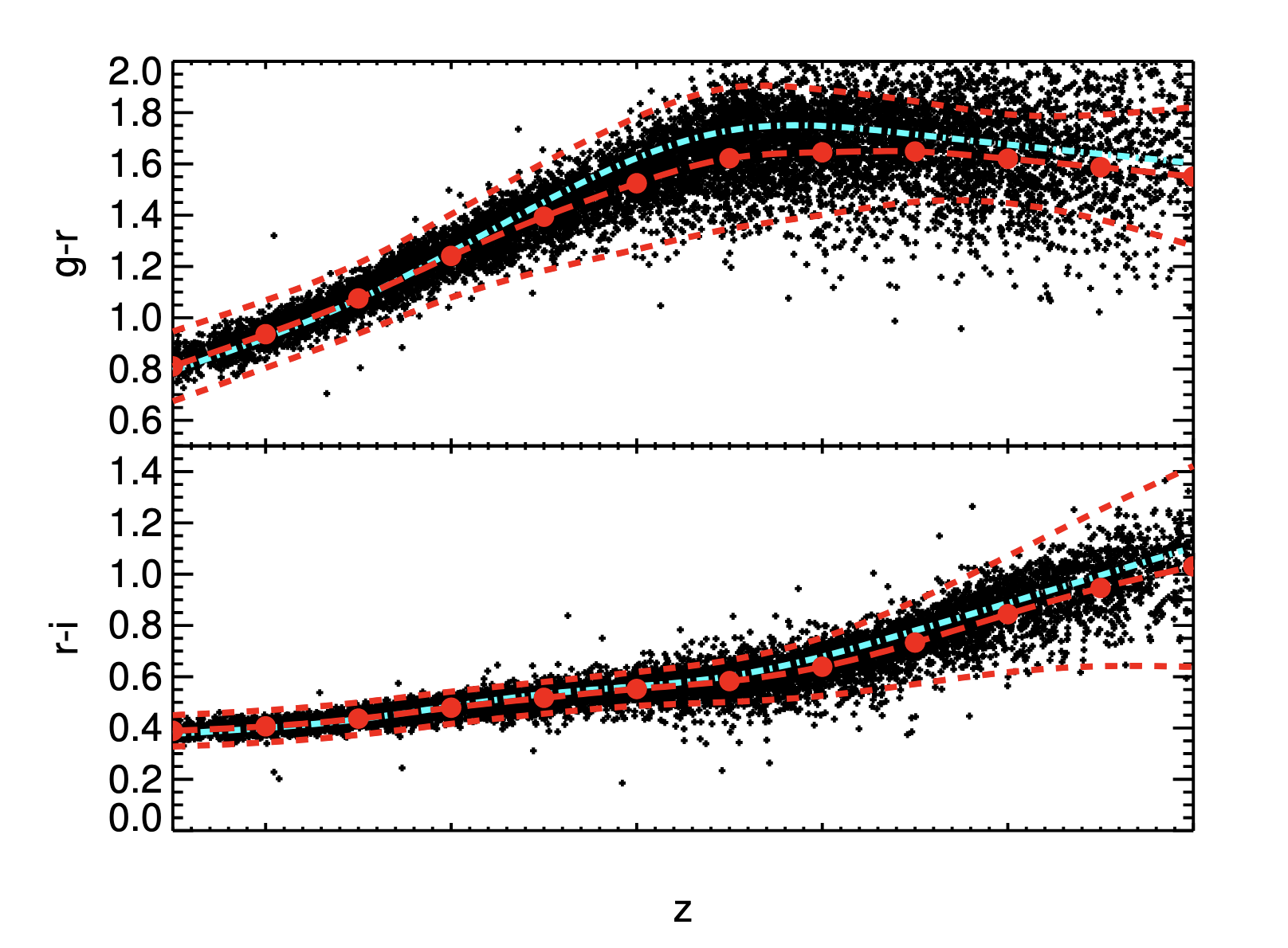
Rykoff2014RedMaPPerAlgorithmSDSS_4.png

6.4.2 Covariance matrix #

这个 section 的目标是计算协方差矩阵的非对角元素

  • 每次计算两种颜色对应的矩阵元素
  • 通过为不同颜色设定优先级顺序来保证矩阵的正定性质
  • 协方差矩阵包括 intrinsic 和 photometric 两部分
    • 前者仅包含一个 band 之间的相关系数 $r$ 作为未知数
      • 对两种颜色之间的相关系数 $r$ 进行一些先验的限制，具体来说是 $\pm0.45$
    • 后者由测光本身的性质给出，其协方差系数来自于颜色计算的共享波段，比如 g-r 和 r-i 中共同的 r

6.5 Iterating the red-sequence model #

将 membership probability 和 red-sequence model 进行迭代的更新直至收敛，因为二者是互相依赖的

  • 在得到 red sequence 参数之后，在测试数据集上运行 cluster finder
    • 仅限于 seed 相关的星系团
    • 最终得到了一个新的列表以及 multi-color 的 membership
  • 然后重新估计 red sequence
  • 对以上过程进行迭代
    • 主要的提升来源于从单色到多色的转变
    • 在多次迭代过程中，平均颜色以及斜率都会很快收敛（3 次）
    • 判断收敛的依据是 richness 不再改变
  • 计算多次迭代的误差变化，在第三次迭代之后偏差都小于 1%
  • 最终用了第三次迭代的输出作为 final cluster catalog

7 Photometric redshift estimation #

在每次迭代的 finder 阶段需要对 cluster 红移进行初始猜测（$z_\mathrm{init}$），以给出 richness 和 membership 的估计

之后可以用全部成员星系对 red sequence 进行拟合，得到红移的更精确估计

7.1 的 $z_\mathrm{red}$ 是针对单个星系，而 7.2 的 $z_\lambda$ 是针对 cluster？

7.1 初始红移 #

  • 对于 SDSS8 可以用多种方法得到 photo-z，但是具有一定的局限性
    • 在 z>0.5 上，photo-z 所需的训练集不足
    • 现有的工具一般目标是给出关于星系红移的统计数据，但是我们需要的是单个星系的红移估计
  • 开发了自己的红移估计方法 $z_\mathrm{red}$
    • 星系的颜色可以转化为 $\chi^2$ 统计量，概率分布和统计量之间的关系是 $P\propto\left(-\frac{1}{2} \chi^2 \right)$
      • 不考虑星系的光度吗？
    • 还考虑了不同红移上的薄片体积大小不同，应该有 $P\propto \frac{\mathrm{d}V}{\mathrm{d}z}$
      • 这个因素类似先验估计，也就是认为星系的体积数密度是恒定的
    • 寻找使以上概率最大的红移，即为红移的初始估计
    • 误差的估计使用后验分布来进行
  • Fig 7 展示了这里 $z_\mathrm{red}$ 的效果
    • 使用了 training galaxy sample
    • 存在一个较小的红移 bias（低估了实际红移）
    • 上面计算出的 error 比实际的 error 更大（蓝线比红线高）
    • 进行修正：将上面的 offset 补偿给原始的估计
      • 感觉有点简陋
      • 仍然存在的 residual 是由于 filter transition

7.2 精确的红移估计 #

实际是上述方法的扩展

在每次迭代中用上一次迭代的红移计算 cluster richness 以及 membership，然后用新的 membership 计算新的红移

在后一步中需要用到一个 likelihood；相比之前的 likelihood，这里还加入了协方差矩阵的行列式以及一次 soft cut

$$ \ln \mathcal{L} = \sum -\frac{w \left[ \chi^2 + \ln |\mathbf{C}| \right]}{2} $$

这里 w 是一个 soft cut 参数（约定以总 richness 的 70% 作为一个截断的阈值）

$$ w(p_{\mathrm{mem}}) = \frac{1}{\exp \left[ (p_{70} - p_{\mathrm{mem}}) / 0.04 \right] + 1} $$

最后可以得到 cluster 红移的后验分布，用高斯拟合这个分布以得到红移估计的误差

  • 在此基础上还进行了基于训练集的校正，以保证红移的估计是无偏的
  • 最后的红移估计结果中存在一些虽然小但是具有较高可信度的偏差（Fig 9）
  • 4000A break 切换颜色的效应体现在红移 0.35~0.45 之间，这也比较接近 SDSS8 的测光深度极限
  • 一些显著较大的偏差是因为 cluster center 的问题
    • 在创建一个 clean sample（14%）之后这些 large offset 消失了（Fig10）
  • Fig12 中展示了红移的概率分布
    • 适当考虑红移概率分布而非简单的估计值之后，红移估计的分布和光谱红移的分布拟合更好

8 Cluster centering #

为星系团确定中心是重要的，因为错误的中心是测量质量和速度弥散的误差的重要来源

这里假设：cluster 中心都有一个 red, bright&dominant galaxy

  • 如果中心星系是 cool-core 的，具有很强的恒星形成，则颜色可能会偏离红色，这是 redMaPPer 的一个已知缺陷
    • 对于 group 更常见，而在 cluster 中比例较低
    • 这个问题可以通过取消对 BCG 的红色限制条件来解决，但是中心定位的效果会下降
    • 另一个方法是用亮度和质量加权平均，但是效果也不好
  • 目前的 centering 成功率大概是 85%

8.1 Basic framework #

不去确定中心的位置，而是计算每一个星系成为 cluster 的概率，从而将中心位置的不确定性也纳入统计的考量

（就算用概率应该也是离散的吧？）

  • 假设 cluster 中的星系分为三类：Central, satellite, unassociated (前景或者背景)
  • 用 filter function 描述三类星系的分布，然后计算星系属于 CG 的 Bayesian 概率
  • 还需要考虑到“cluster 只具有一个 CG”的条件

8.2 Centering filters #

介绍三种星系的 filter function 如何定义

  • 星系的性质用星等、红移、权重来描述
    • 权重用于描述周围星系的密度
    • 前面用到的星系性质 vertor $\mathbf{x}$ 都是位置、颜色、星等
      • 用红移代替了颜色，因为红移受到的干扰更小
      • 用权重替代了位置
  • 对于 CG
    • 星等用一个 Gaussian 定义，其中星等的均值依赖于红移
      • 这里的 $m_\star(z)$ 是 Schechter 函数的参数
    • 红移也用一个 Gaussian 定义
      • 这里 $z_\mathrm{red}$ 是星系测光红移，而 $z_\lambda$ 是 cluster 红移
      • 衡量星系和 cluster 之间的红移差距
    • 权重 w 由周围的星系的贡献相加得到
      • 对于 richness 和红移不存在依赖
      • 同样使用一个 Gaussian filter function
  • 对于 satellite 来说 filter function 基本和 CG 相同，除了——
    • 更合适的 weight 参数（为什么 satellite 也要考虑周围的星系密度？）
    • 光度函数采用 Schechter function
  • 对背景来说，filter function 由平均密度乘角度区域的大小得到

8.3 Implementation #

需要确定以上函数中的参数

用迭代方法同时限制 center 和 red sequence model

8.4 Blue central galaxy #

如果中心星系颜色比较蓝，那么 redMaPPer 会错误地将周围的红色星系作为 CG

一个例子是 Abell 1835

这种情况的比例低于 2%

9 Cluster finder #

大概明白了，也就是 sec 4,5 作为 6 的 ingredient, 而 7,8 作为 9 的 ingredient

前面讨论了一个 finder 的全部组分，现在开始组装

具体的步骤是：

  • 估计一个红移 $z_\mathrm{red}$，寻找周围的 over-density
  • 计算每一个 over-density 属于 cluster 的概率
  • 对星系团进行 percolate

9.1 First pass #

就是先粗略过一遍

  • 用非常宽松的条件减少需要检查的星系数量（56m -> 23m）
  • 计算潜在 CG 的红移 $z_\mathrm{red}$ 以及 richness $\lambda$，排除 richness 太低的星系
    • 这一步拒绝了 60% 的星系
  • 基于 7.2 的方法校准更精确的红移

9.2 Likelihood sorting #

基于通过 pass 的星系 catalog 计算 richness，然后计算 lambda likelihood

完整的 likelihood 由 lambda 和 center 两部分组成，后者由 sec8 给出

前一个 likelihood 占据主导地位

9.3 Percolation #

将星系分配给 cluster，同时避免重复计数

具体的过程是：对每一个星系

  • 由于 catalog 中已经有被排除的星系，对潜在的 CG 重新计算红移和 richness
  • 确定 cluster 中心（sec8）
  • 基于新确定的中心重新计算红移和 richness
  • 从 catalog 中移除已经被归类到 cluster 中的星系

9.3.1 Masking #

在对 catalog 进行逐一检查的过程中，一个星系属于前面已经检验过的 cluster 的概率会逐渐增加，这会导致星系属于其他 cluster 的概率下降，这体现在后续 cluster 的 richenss 计算过程中

假设一个星系有 0.3 的概率属于前面的一个星系团，它在计算后续排序的时候就只能用 0.7 的概率分配给其他的 cluster

如果 cluster 彼此之间重叠程度很小，以上的修正影响不大

9.3.2 Extent of Clusters and Percolation Radius #

this work 使用了和 richness 相关的 aperture radius

另一个有意义的半径是 percolation radius，这个值和宇宙学参数 $R_\mathrm{200}$ 有关

R12 中研究了 maxBCG catalog，发现 $R_\mathrm{200}\approx1.5R_C(\lambda)$，所以在这里使用了 $1.5R_C(\lambda)$ 作为 percolation radius

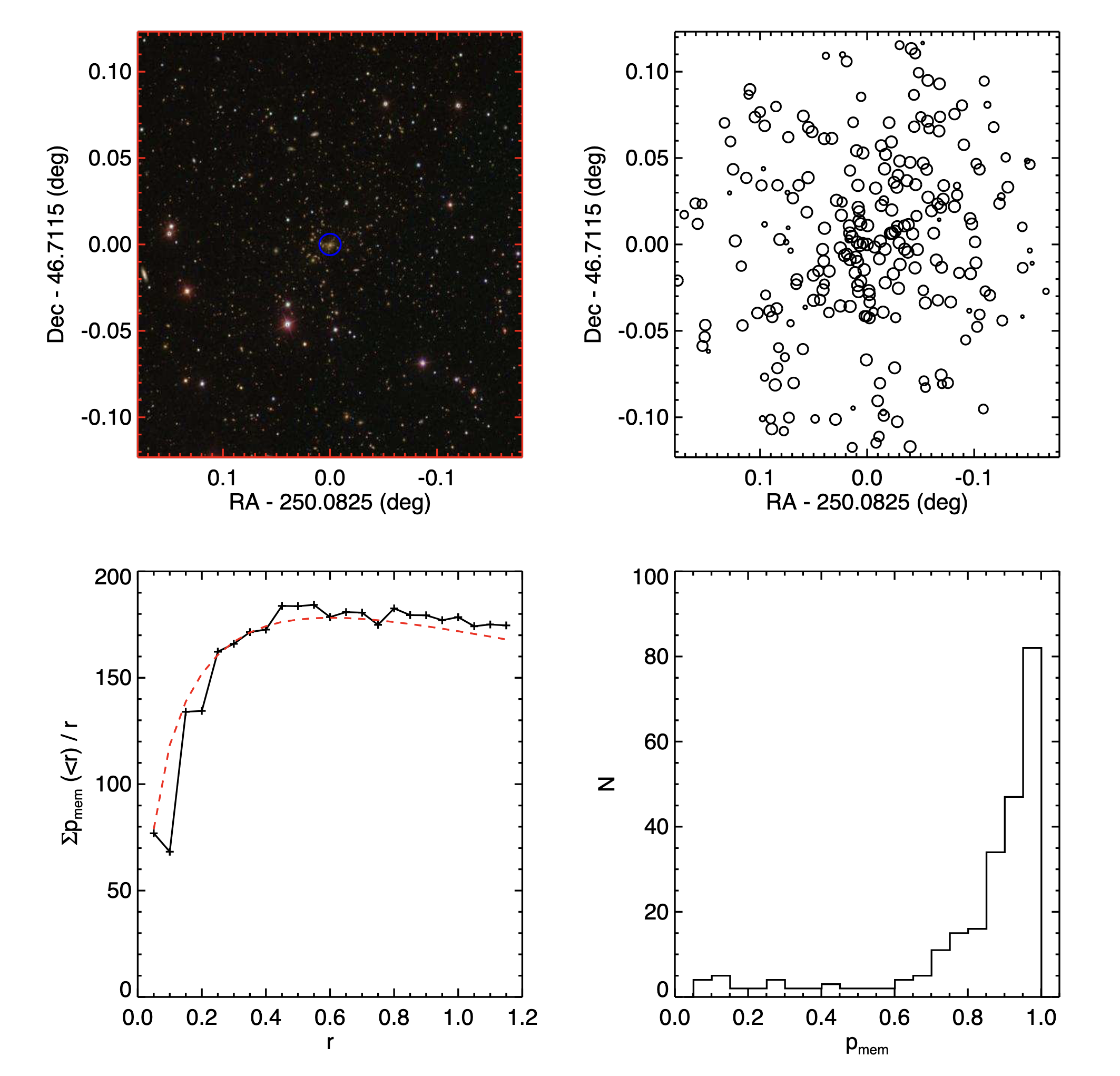
9.4 A sample #

一个 z=0.23 的星系团，这里给出了 SDSS 图像、位置分布、到 cluster 中心的距离、membership probability 的分布

星系密度的分布符合 NFW distribution

Rykoff2014RedMaPPerAlgorithmSDSS_5.png

10 Catalog #

对 cluster catalog 进行了一些红移、richness 以及 mask fraction 的限制

最终 catalog 包含 25236 个 cluster

在 0.35 以下是 volume limited 的

11 Purity&completeness #

用一些 mock 方法进行检测

12 Cluster masks #

用 mock 探寻 bright star 的影响

可以用 random cluster point 来绘制探测能力 map

cluster mask 和 galaxy mask 之间的差异？

13 Summary #

redMaPPer 在将来可以用于 DES 和 LSST

  • richness $\lambda$ 被证明是一种很好的 mass proxy
  • redMaPPer 需要训练光谱作为输入，但是需求量不大
  • 给出 cluster 的位置的概率分布，适用于统计研究

下一篇 paper 比较了这里的 catalog 和 SZ/X-ray catalog 的区别

back to top